🌸
A Fibonacci Szám / 1.618 033 988 749 894 848
🌸
🌸
🌸
Ha megnézzük a napraforgó fejét, spirál alakzatokat fedezhetünk fel benne,
egészen pontosan 21 - et vagy 34 - et, attól függően, melyik irányból nézzük.
Ha megnézzük a napraforgó fejét, spirál alakzatokat fedezhetünk fel benne,
egészen pontosan 21 - et vagy 34 - et, attól függően, melyik irányból nézzük.
🌸
Leonardo Bonacci, Leonardo Fibonacci
🌸
Született. 1170 – 75 / Elhunyt. 1240 – 50 / Valószínűleg Pizzában.
https://hu.wikipedia.org/wiki/Fibonacci
Fibonacci, más néven Leonardo di Pisa vagy Leonardo Pisano,
Leonardo Bonacci, Leonardo Fibonacci (Pisa, kb. 1170 – kb. 1250) itáliai matematikus.
Leginkább arról nevezetes, hogy ő terjesztette el a hindu–arab számírást Európában a Liber Abaci című könyvével.
A róla elnevezett Fibonacci-számokat nem ő fedezte fel,
de példaként használta ugyanebben a művében.
Leonardo Bonacci, Leonardo Fibonacci
🌸
Született. 1170 – 75 / Elhunyt. 1240 – 50 / Valószínűleg Pizzában.
https://hu.wikipedia.org/wiki/Fibonacci
Fibonacci, más néven Leonardo di Pisa vagy Leonardo Pisano,
Leonardo Bonacci, Leonardo Fibonacci (Pisa, kb. 1170 – kb. 1250) itáliai matematikus.
Leginkább arról nevezetes, hogy ő terjesztette el a hindu–arab számírást Európában a Liber Abaci című könyvével.
A róla elnevezett Fibonacci-számokat nem ő fedezte fel,
de példaként használta ugyanebben a művében.
🌸
Fibonacci számok a természetben
http://www.nigro.hu/2011/08/08/fibonacci-szamok-a-termeszetben/
Talán ismerős a név, hisz a matematika egy ismert sorozatáról van szó. Azonban sokan vélnek összefüggést látni a Fibonacci számok és a természet sorozatai közt.
A sorozatot először 1150-ben írta le két indiai matematikus, Gopala és Hemacsandra, akik a szanszkrit költészet elméleti kérdéseit vizsgálva ütköztek egy összegre bontási problémába (hányféleképpen lehet rövid és hosszú szótagokkal kitölteni egy adott időtartamot, ha egy hosszú szótag két rövidnek felel meg?).
Nyugaton tőlük függetlenül találta meg 1202-ben Fibonacci, aki Liber Abaci (Könyv az abakuszról) című művében ír róla.
Fibonacci számok a természetben
http://www.nigro.hu/2011/08/08/fibonacci-szamok-a-termeszetben/
Talán ismerős a név, hisz a matematika egy ismert sorozatáról van szó. Azonban sokan vélnek összefüggést látni a Fibonacci számok és a természet sorozatai közt.
A sorozatot először 1150-ben írta le két indiai matematikus, Gopala és Hemacsandra, akik a szanszkrit költészet elméleti kérdéseit vizsgálva ütköztek egy összegre bontási problémába (hányféleképpen lehet rövid és hosszú szótagokkal kitölteni egy adott időtartamot, ha egy hosszú szótag két rövidnek felel meg?).
Nyugaton tőlük függetlenül találta meg 1202-ben Fibonacci, aki Liber Abaci (Könyv az abakuszról) című művében ír róla.
Mik is azok a Fibonacci számok?
https://hu.wikipedia.org/wiki/Fibonacci-számok
Az első két elem 0 és 1, a további elemeket az előző kettő összegeként kapjuk.
🌸
Képletben:
0, ha n = 0,
F(n) = 1, ha n = 1,
F(n-1) + F(n-2), ha n > 1
Nem kell megijedni, nem lesz bonyolult, csak a szokásos “matekos ijesztgetős” képletet láthatjátok. Pár perc múlva már egyértelmű lesz az egész
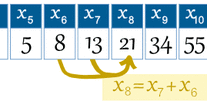
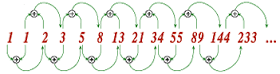
Tehát így néznek ki a számok: 0,1,1,2,3,5,8,13,21,34,55,89,…. stb (tehát minden előző két szám összege adja meg a következő számot. )
Eddig azért semmi izgalom. Uncsi matek. Node! Kepler 1611-es könyvében, a The Six-Cornered Snowflake-ben újra felfedezte, és különféle természeti jelenségekkel hozta kapcsolatba. Nocsak.
Ez már mindjárt kezd így érdekesnek hangzani. Ugyanis kiderült, hogy a szomszédos Fibonacci-számok aránya, az aranymetszés értékéhez tart.
Azt pedig szeretjük, hisz az akvárium berendezésének alapja. Persze van még sok más összefüggés is a természettel, pl: A virágszirmok száma gyakran Fibonacci-szám: például a liliomnak, a nősziromnak és a hármassziromnak három; a haranglábnak, a boglárkának, a larkspurnak és a vadrózsának öt; a szarkalábnak, a vérpipacsnak és a pillangóvirágnak nyolc; a jakabnapi aggófűnek, a hamvaskának és a körömvirágnak 13; az őszirózsának, a borzas kúpvirágnak és a cikóriának 21; a fodroslevelű margitvirágnak, az útilapunak és egyes százszorszépeknek 34; más százszorszép-fajoknak pedig 55 vagy 89 szirma van.
https://hu.wikipedia.org/wiki/Fibonacci-számok
Az első két elem 0 és 1, a további elemeket az előző kettő összegeként kapjuk.
🌸
Képletben:
0, ha n = 0,
F(n) = 1, ha n = 1,
F(n-1) + F(n-2), ha n > 1
Nem kell megijedni, nem lesz bonyolult, csak a szokásos “matekos ijesztgetős” képletet láthatjátok. Pár perc múlva már egyértelmű lesz az egész
Tehát így néznek ki a számok: 0,1,1,2,3,5,8,13,21,34,55,89,…. stb (tehát minden előző két szám összege adja meg a következő számot. )
Eddig azért semmi izgalom. Uncsi matek. Node! Kepler 1611-es könyvében, a The Six-Cornered Snowflake-ben újra felfedezte, és különféle természeti jelenségekkel hozta kapcsolatba. Nocsak.
Ez már mindjárt kezd így érdekesnek hangzani. Ugyanis kiderült, hogy a szomszédos Fibonacci-számok aránya, az aranymetszés értékéhez tart.
Azt pedig szeretjük, hisz az akvárium berendezésének alapja. Persze van még sok más összefüggés is a természettel, pl: A virágszirmok száma gyakran Fibonacci-szám: például a liliomnak, a nősziromnak és a hármassziromnak három; a haranglábnak, a boglárkának, a larkspurnak és a vadrózsának öt; a szarkalábnak, a vérpipacsnak és a pillangóvirágnak nyolc; a jakabnapi aggófűnek, a hamvaskának és a körömvirágnak 13; az őszirózsának, a borzas kúpvirágnak és a cikóriának 21; a fodroslevelű margitvirágnak, az útilapunak és egyes százszorszépeknek 34; más százszorszép-fajoknak pedig 55 vagy 89 szirma van.
Fibonacci-spirálba rendeződnek például a fenyőtoboz és az ananász pikkelyei, a napraforgó magjai, a málna szemei, a karfiol rózsái és egyes kaktuszok tüskéi. A nautiluszok háza is hasonlít a Fibonacci-spirálhoz, de nem egy negyed, hanem egy teljes kör alatt nő meg a sugár phi,-szeresére. Hohó, de mi az a Fibonacci spirál?
🌸
🌸
A Fibonacci - Spirál
egy olyan logaritmikus spirál, ami egy negyedfordulat alatt nő a phi,-szeresére. Jól közelíthető az arany téglalap segítségével (remélem mindenki az arany téglalapra koncentrál… ).
A Fibonacci-spirálon egyenlő távolságra pontokat elhelyezve azok „spirálkarokká” állnak össze, és ezen karok száma Fibonacci-szám lesz.
A Fibonacci-spirál mentén elhelyezett gömbök optimális elrendezést adnak abban az értelemben, hogy nagyon sok gömböt elhelyezve is azok egyenletesen oszlanak el.
egy olyan logaritmikus spirál, ami egy negyedfordulat alatt nő a phi,-szeresére. Jól közelíthető az arany téglalap segítségével (remélem mindenki az arany téglalapra koncentrál… ).
A Fibonacci-spirálon egyenlő távolságra pontokat elhelyezve azok „spirálkarokká” állnak össze, és ezen karok száma Fibonacci-szám lesz.
A Fibonacci-spirál mentén elhelyezett gömbök optimális elrendezést adnak abban az értelemben, hogy nagyon sok gömböt elhelyezve is azok egyenletesen oszlanak el.
Akkor ezek után nincs más hátra, minthogy megnézzünk néhány verseny akváriumot.
Állnak-e ezek a szabályok?
Állnak-e ezek a szabályok?
🌸
Ahogy észrevettem, az egykompozíciós elrendezéseknél működik.
🌸
Ahogy észrevettem, az egykompozíciós elrendezéseknél működik.
🌸
Persze ez ritkán tudatos, inkább csak az ember érzékei diktálnak, de érdemes időnként így is megvizsgálni a dolgokat. Bartók műveiben is felfedezhetőek az egyes zenei gondolatok ütemsorrendjében, melyet nem tudatosan, hanem ösztönösen alakított így.
Néha azért az az érzésem, hogy egyes matematikusok nem tudnak mit kezdeni a számaikkal és igyekszenek mindenben valami összefüggést látni, de azért érdekes…
Néha azért az az érzésem, hogy egyes matematikusok nem tudnak mit kezdeni a számaikkal és igyekszenek mindenben valami összefüggést látni, de azért érdekes…
Fibonacci Nyulai
http://www.jgytf.u-szeged.hu/tanszek/matematika/speckoll/1998/fibonacci/folap.htm
Összeállította: Herold Zsuzsa
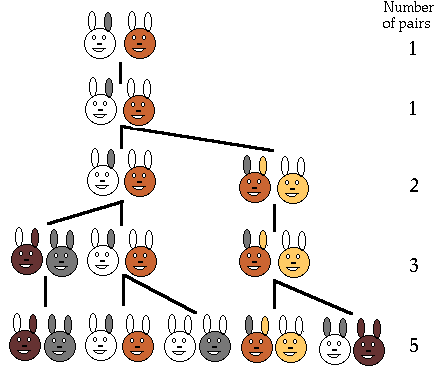
Az eredeti probléma, amelyet Fibonacci kutatott (1202) arról szólt, hogy ideális körülmények között a nyulak milyen gyorsan, milyen rendszerességgel ellenek.
Tegyük fel, hogy egy mezõn él egy újszülött nyúl pár, egy hím és egy nõstény. A nyulak egy hónapos korukra lesznek ivarérettek, így a második hónap végén már megszülethetnek az elsõ kicsinyek.
Tegyük fel, hogy a mi nyulaink soha nem halnak meg és hogy a nõstények mindig új párt ellenek ( 1 hímet és 1 nõstényt) minden hónapban, a második hónaptól kezdve.
Fibonacci problémája: hány pár lesz egy éven belül?
1. Az elsõ hónap végén még csak 1 pár van.
2. A második hónap végén születik 1 új pár, így most már 2 pár van.
3. A harmadik hónap végén az eredeti nõsténynek születik a második pár nyula, így már 3 pár lesz.
4. A negyedik hónap végén az eredeti nõsténynek lesz újabb kicsinye, a második hónapban született nõstény most elli az elsõ kicsinyeit, így összesen már 5 pár nyúl van.
http://www.jgytf.u-szeged.hu/tanszek/matematika/speckoll/1998/fibonacci/folap.htm
Összeállította: Herold Zsuzsa
Az eredeti probléma, amelyet Fibonacci kutatott (1202) arról szólt, hogy ideális körülmények között a nyulak milyen gyorsan, milyen rendszerességgel ellenek.
Tegyük fel, hogy egy mezõn él egy újszülött nyúl pár, egy hím és egy nõstény. A nyulak egy hónapos korukra lesznek ivarérettek, így a második hónap végén már megszülethetnek az elsõ kicsinyek.
Tegyük fel, hogy a mi nyulaink soha nem halnak meg és hogy a nõstények mindig új párt ellenek ( 1 hímet és 1 nõstényt) minden hónapban, a második hónaptól kezdve.
Fibonacci problémája: hány pár lesz egy éven belül?
1. Az elsõ hónap végén még csak 1 pár van.
2. A második hónap végén születik 1 új pár, így most már 2 pár van.
3. A harmadik hónap végén az eredeti nõsténynek születik a második pár nyula, így már 3 pár lesz.
4. A negyedik hónap végén az eredeti nõsténynek lesz újabb kicsinye, a második hónapban született nõstény most elli az elsõ kicsinyeit, így összesen már 5 pár nyúl van.
A párok száma
Minden hónap elején a nyúlpárok száma: 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Megoldás
Miért egyeznek meg a Fibonacci számok a nyúlpárok számával minden hónapban?
Miért ez a válasz a "nyúl-problémára"?
f(n) legyen a mezõn élõ nyulak száma az n-dik hónap elején.
Megmutatjuk, hogy f(1) = 1, f(2) = 1 és f(n) = f(n-1) + f(n-2) , amely pontosan a Fibonacci számok definíciójával egyezik meg. ( Teljesül f(0) = 0 is.)
Kezdjük az elsõ hónappal, amikor még csak az újszülött pár van:
f(1)=1
A második hónapban is mégcsak az 1.pár van:
f(2)=1
Feltételünk szerint az 1.pár a harmadik hónap elején születik meg. Tehát mennyi nyúl lesz 2 hónap után? Mi f(n)?
Minden elõzõ hónapban élõ nyúl (f(n-1)) él a következõben is, tehát legalább f(n-1) van.
Mennyi új születik?
Minden pár, amely már két hónapja is élt, képes újat elleni és feltesszük, hogy minden hónapban csak egyet. Mivel minden nyúl vagy az elmúlt hónapokban született, vagy most:
f(n)=f(n-1)+f(n-2), ha n>2
Ez pontosan a Fibonacci számok definíciója (0 -val és 1 -gyel kezdve).
Hogyan lehet még szemléltetni a Fibonacci számokat?
Rajzoljunk két 1 egységnyi oldalú négyzetet egymás mellé, melyeknek egyik oldaluk érinti egymást. Ezek fölé kétegységnyi oldalhosszúságú négyzetet (2=1+1).
🌸
Minden hónap elején a nyúlpárok száma: 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Megoldás
Miért egyeznek meg a Fibonacci számok a nyúlpárok számával minden hónapban?
Miért ez a válasz a "nyúl-problémára"?
f(n) legyen a mezõn élõ nyulak száma az n-dik hónap elején.
Megmutatjuk, hogy f(1) = 1, f(2) = 1 és f(n) = f(n-1) + f(n-2) , amely pontosan a Fibonacci számok definíciójával egyezik meg. ( Teljesül f(0) = 0 is.)
Kezdjük az elsõ hónappal, amikor még csak az újszülött pár van:
f(1)=1
A második hónapban is mégcsak az 1.pár van:
f(2)=1
Feltételünk szerint az 1.pár a harmadik hónap elején születik meg. Tehát mennyi nyúl lesz 2 hónap után? Mi f(n)?
Minden elõzõ hónapban élõ nyúl (f(n-1)) él a következõben is, tehát legalább f(n-1) van.
Mennyi új születik?
Minden pár, amely már két hónapja is élt, képes újat elleni és feltesszük, hogy minden hónapban csak egyet. Mivel minden nyúl vagy az elmúlt hónapokban született, vagy most:
f(n)=f(n-1)+f(n-2), ha n>2
Ez pontosan a Fibonacci számok definíciója (0 -val és 1 -gyel kezdve).
Hogyan lehet még szemléltetni a Fibonacci számokat?
Rajzoljunk két 1 egységnyi oldalú négyzetet egymás mellé, melyeknek egyik oldaluk érinti egymást. Ezek fölé kétegységnyi oldalhosszúságú négyzetet (2=1+1).
🌸
🌸
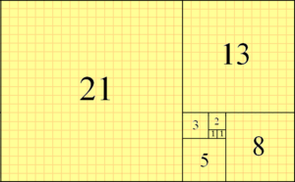
Ezután folytathatjuk a 3 egységnyi oldalhosszúságúval, amely az elõzõt érinti...
Ezt így folytathatjuk tovább. Minden oldalhosszúság az elõzõ 2 összegével egyezik meg. Ezen négyszögeknek az oldalhosszúságai Fibonacci számok, ezért ezeket Fibonacci négyszögeknek nevezzük.
A következõ ábra megmutatja, hogy hogyan lehet negyed körívekbõl spirált rajzolni úgy, hogy minden négyzetben egy negyed körív legyen.
🌸
Ezután folytathatjuk a 3 egységnyi oldalhosszúságúval, amely az elõzõt érinti...
Ezt így folytathatjuk tovább. Minden oldalhosszúság az elõzõ 2 összegével egyezik meg. Ezen négyszögeknek az oldalhosszúságai Fibonacci számok, ezért ezeket Fibonacci négyszögeknek nevezzük.
A következõ ábra megmutatja, hogy hogyan lehet negyed körívekbõl spirált rajzolni úgy, hogy minden négyzetben egy negyed körív legyen.
🌸

Ezt Fibonacci spirálnak nevezzük.

Hasonló alakzatok a természetben is megjelennek csigaházakon,
kagylókon:
kagylókon:
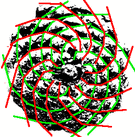
A fenyõ tobozain is felfedezhetõ a Fibonacci spirál:
A piros vonalak mutatják az egyik irányt, a zöldek a másikat.
A Fibonacci számok a természet ezernyi területén megjelennek,
mint például növények leveleinek elrendezésében a száron,
ás a virágok szirmainak száma is Fibonacci szám.
A piros vonalak mutatják az egyik irányt, a zöldek a másikat.
A Fibonacci számok a természet ezernyi területén megjelennek,
mint például növények leveleinek elrendezésében a száron,
ás a virágok szirmainak száma is Fibonacci szám.
🌸
0, 1 + 1 = 2 / 1 + 2 = 3 / 2 + 3 = 5 / 3 + 5 = 8. STB. 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
🌸
🌸
Az Élet Virága
Modern elnevezése annak a geometrikus formának, melyben egymást megfelelően fedő - és egyenletesen eloszló körök egy virágszerű mintázatot hoznak létre hatszoros szimmetriával, mint egy hatszögnél.
Minden kör középpontja az őt körülvevő 6 másik kör kerületén helyezkedik el. Az Élet Virága világszerte, sok kultúrában - régen és most is - szent szimbólum.
Az univerzum leképeződésének tekintik, mivel például mindazon építőkövét megtalálhatjuk a szimbólumban amit szabályos testnek nevezünk.
A szimbólumot olyan metafóraként foghatjuk fel, mint amelyik az univerzum szellemének és minden életnek az összekapcsolódását ábrázolja.
http://www.eletesegeszseg.com/eacutelet-viraacutega.html
Az Élet Virága
Modern elnevezése annak a geometrikus formának, melyben egymást megfelelően fedő - és egyenletesen eloszló körök egy virágszerű mintázatot hoznak létre hatszoros szimmetriával, mint egy hatszögnél.
Minden kör középpontja az őt körülvevő 6 másik kör kerületén helyezkedik el. Az Élet Virága világszerte, sok kultúrában - régen és most is - szent szimbólum.
Az univerzum leképeződésének tekintik, mivel például mindazon építőkövét megtalálhatjuk a szimbólumban amit szabályos testnek nevezünk.
A szimbólumot olyan metafóraként foghatjuk fel, mint amelyik az univerzum szellemének és minden életnek az összekapcsolódását ábrázolja.
http://www.eletesegeszseg.com/eacutelet-viraacutega.html
Miért pont a Fibonacci számok
mozgatják a világmindenséget?
Mindenütt ott vannak.
A gabonaköröktől a csigaháztól a fülkagylónkon át a galaxisokig szinte minden spirális képződményben. De vajon honnan ismeri a mikro és makrokozmosz a Fibonacci sorozatot? Netán a világmindenséget ez alapján teremtette a Mindenható?
mozgatják a világmindenséget?
Mindenütt ott vannak.
A gabonaköröktől a csigaháztól a fülkagylónkon át a galaxisokig szinte minden spirális képződményben. De vajon honnan ismeri a mikro és makrokozmosz a Fibonacci sorozatot? Netán a világmindenséget ez alapján teremtette a Mindenható?
Galilelo Galileo mondta volt, hogy a „természet nagy könyve a matematika nyelvén íródott”.
Ennek mi sem szolgál ékesebb bizonyítékaként, minthogy nyitott szemmel járva a világban, lépten-nyomon ugyanabba a rejtélyes számsorba botlunk, akár Robert Langdon a Da Vinci kódban, mégpedig a Fibonacci számsorba.
A számsor lényege, hogy minden szám az azt megelőző két szám összege, azaz:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
Tényleg mindenütt jelen vannak?
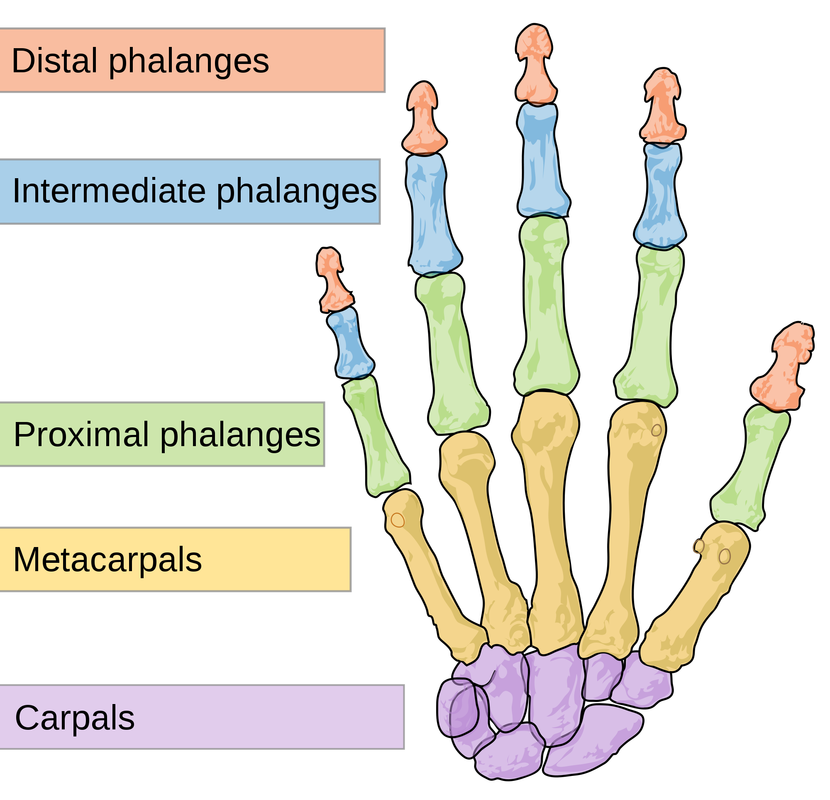
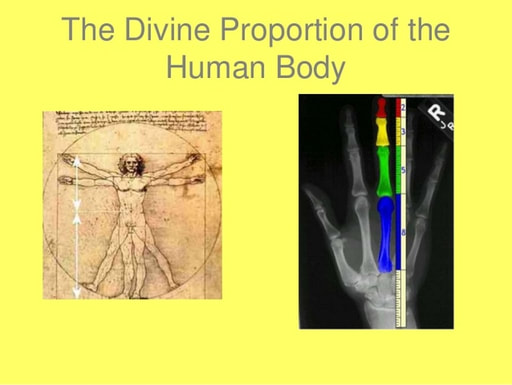
Ahhoz, hogy belássuk, milyen szinten van jelen a számsor mindennapi életünkben, elég, ha ránézünk saját kezünkre. 2 kezünkön 5 ujjunk van és mindegyik ujjunkon 3 ujjpercünk, ágyéki csigolyánk pedig nem több, nem kevesebb csontból áll, mint 5-ből.
Számos virág szirmainak száma valamilyen Fibonacci szám, például a kálának 1, a boglárkának 5, a százszorszépnek pedig gyakran 34 vagy 55 szirma van.
A varázslatos számsor a zenében is elkísér minket. Ha csak a kromatikus skálára tekintünk, 13 félhangból áll, amelyet a zongora billentyűire nézve (mely ennek legkézenfekvőbb vizuális szemléltetése) pontosan 5 fekete és 8 fehér billentyűzet alkot. A legszebben csengő dúr akkord pedig sorrendben az 1-ső, 5-dik és 8-dik (sic!) hang együttes megszólaltatásával érhető el.
De felkaphatják a fejüket Douglas Adams rajongói is, hiszen a világmindenség értelmének kikiáltott 42-es szám nem más, mint a Fibonacci számsorozatban egymás után következő 8+13+21 összege. Sőt, másik két Fibonacci szám összege a 34 és a 8 összege is ugyanezt a számot adja eredményül.
🌸
Ennek mi sem szolgál ékesebb bizonyítékaként, minthogy nyitott szemmel járva a világban, lépten-nyomon ugyanabba a rejtélyes számsorba botlunk, akár Robert Langdon a Da Vinci kódban, mégpedig a Fibonacci számsorba.
A számsor lényege, hogy minden szám az azt megelőző két szám összege, azaz:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 …
Tényleg mindenütt jelen vannak?
Ahhoz, hogy belássuk, milyen szinten van jelen a számsor mindennapi életünkben, elég, ha ránézünk saját kezünkre. 2 kezünkön 5 ujjunk van és mindegyik ujjunkon 3 ujjpercünk, ágyéki csigolyánk pedig nem több, nem kevesebb csontból áll, mint 5-ből.
Számos virág szirmainak száma valamilyen Fibonacci szám, például a kálának 1, a boglárkának 5, a százszorszépnek pedig gyakran 34 vagy 55 szirma van.
A varázslatos számsor a zenében is elkísér minket. Ha csak a kromatikus skálára tekintünk, 13 félhangból áll, amelyet a zongora billentyűire nézve (mely ennek legkézenfekvőbb vizuális szemléltetése) pontosan 5 fekete és 8 fehér billentyűzet alkot. A legszebben csengő dúr akkord pedig sorrendben az 1-ső, 5-dik és 8-dik (sic!) hang együttes megszólaltatásával érhető el.
De felkaphatják a fejüket Douglas Adams rajongói is, hiszen a világmindenség értelmének kikiáltott 42-es szám nem más, mint a Fibonacci számsorozatban egymás után következő 8+13+21 összege. Sőt, másik két Fibonacci szám összege a 34 és a 8 összege is ugyanezt a számot adja eredményül.
🌸
🌸
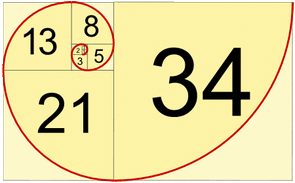
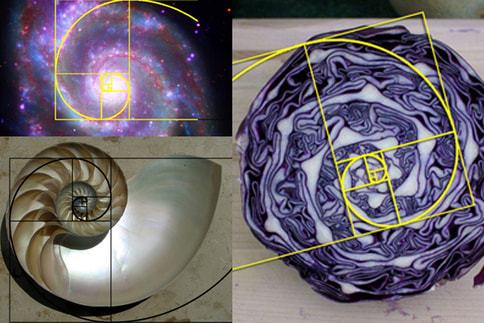
Ha pedig ezeket a számokat négyszögek oldalának hosszaként használjuk fel, a négyszögeket egymás mellé rakjuk és pontjaikat körívekkel összekötjük, akkor az aranyspirálhoz jutunk, amelyet a természet megannyi csodálatos teremtményében, sőt a világegyetemben is felfedezhetünk.
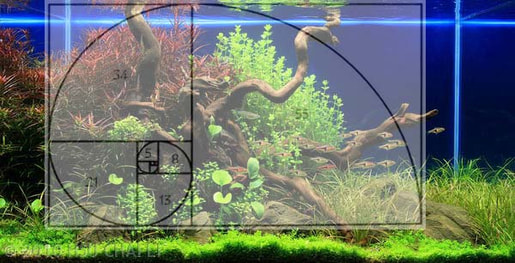
Ha megnézzük a napraforgó fejét, spirál alakzatokat fedezhetünk fel benne, egészen pontosan 21-et vagy 34-et, attól függően, melyik irányból nézzük. Az ananász esetében szintén felfedezhetjük a spirálokat, szám szerint 8-at illetve 13-at. Ugyanerre a spirálra ismerhetünk rá a Nautilus kagylóban vagy éppen a fejes káposztában. De, ha távolabbra tekintünk, a spirálgalaxisok is rendszerint ugyanezt az alakzatot mutatják.
🌸
Ha pedig ezeket a számokat négyszögek oldalának hosszaként használjuk fel, a négyszögeket egymás mellé rakjuk és pontjaikat körívekkel összekötjük, akkor az aranyspirálhoz jutunk, amelyet a természet megannyi csodálatos teremtményében, sőt a világegyetemben is felfedezhetünk.
Ha megnézzük a napraforgó fejét, spirál alakzatokat fedezhetünk fel benne, egészen pontosan 21-et vagy 34-et, attól függően, melyik irányból nézzük. Az ananász esetében szintén felfedezhetjük a spirálokat, szám szerint 8-at illetve 13-at. Ugyanerre a spirálra ismerhetünk rá a Nautilus kagylóban vagy éppen a fejes káposztában. De, ha távolabbra tekintünk, a spirálgalaxisok is rendszerint ugyanezt az alakzatot mutatják.
🌸
🌸
Ki volt Fibonacci?
Az 1170 és 1250 között élt itáliai matematikus, Leonardo di Pisa (ma ismert nevén Leonardo Fibonacci) valószínűleg sosem gondolta volna, hogy az internet és a kreacionizmus látens híveinek köszönhetően ilyen legendássá válik az egyébként már a 6. századi Indiában is ismert számsorozat.
A XII. század Itáliájában még mindig a római számokat használták, amely igencsak megnehezítette a számokkal foglalkozók, elsősorban kereskedők életét. Leonardo maga is megtapasztalhatta ezt, amikor apjának segített, aki kereskedelmi ügyvivő volt az Almohád-Dinasztia szultánusában, a mai Algéria területén. Itt botlott bele az ifjú Leonardo az arabok által használt tízes számrendszerbe, amellyel sokkal egyszerűbben és hatékonyabban lehetett számolni.
Több arab matematikusnál tanult, hogy minél jobban elmélyedjen a tízes számra az arab számok tudományában, majd 1200 körül hazatérve Liber Abaci című művében kezdje népszerűsíteni azokat.
A könyv a tízes számrendszer és vele való műveletek ismertetésén túl számos gyakorlati útmutatót kínált az élet különböző területeire, a súlyok és mértékegységek átváltásától a tőkekalkulációkon keresztül egészen a nyúltenyészet elméleti növekedési görbéjének meghatározásáig. Ez utóbbihoz használt, meglehetősen erőltetett példával vezette be az európai köztudatba az azóta misztikussá váló számsort, amelyet az iránta való tiszteletből róla neveztek el.
Miért vannak jelen mindenütt?
Valójában éppannyira vannak jelen, mint számos egyéb mintázat, amelyet matematikai modellekkel le tudunk írni. A misztikum azonban, amelyre cikkünk elején mi is példákat hoztunk fel, nem más, mint szemfényvesztés, egyszerű bűvészmutatvány. Kiragadott példákat kerestünk a Fibonacci számokra illetve a Fibonacci spirálra, nagyvonalúan elfeledkezve mindazon esetekről, amikor a Fibonacci rejtélyt semmilyen módon sem tudnánk ráerőltetni a természetre.
33 darab csigolyánk van, nyakcsigolyánk 7, hátcsigolyánk pedig 12. Egyikük sem Fibonacci szám. Ahogyan számos virágnak a Fibonacci számtól eltérő számú szirma van (pl. liliom 6, gardénia 9, hegyi babér 10).
Nem magyaráztuk meg, miért 12 hangból áll egy oktáv, ahogyan azt sem, hogy a fülbemászó melankolikus dallamok elengedhetetlen kelléke, a moll akkord miért az 1-ső 4-dik és 8-dik (sic!) billentyű lenyomásával szólaltatható meg.
Szándékosan elfelejtettük megemlíteni a számsor néhány fontos matematikai törvényszerűségét. Egyrészt, hogy bármely egész szám felírható Fibonacci számok segítségével, másrészt bármely szám előállítható két vagy több olyan Fibonacci szám összeadásával, amelyek nem szomszédai egymásnak. Így nem okozott különösebb nehézséget a 42-t egymást követő, illetve egymással nem szomszédos Fibonacci számokból előállítani.
A spirális alakzatok tekintetében szintén csaltunk. Szándékosan olyan képeket közöltünk, ahol szabad szemmel nem megállapítható a különbség, csak ha egymásra tennénk a képet és a spirált.
A Fibonacci spirált gyakran hasonlítják az ún. aranyspirálhoz, amely nem más, mint az aranymetszésből ismert Fibonacci alapú logaritmikus spirál. Természettudósok szerint a logaritmikus spirál mintázatát valóban sok élőlény próbálja követni, azon egyszerű oknál fogva, hogy ez a legjobb módszer az arányos növekedésre, a napraforgó tányérja esetében pedig megközelítőleg a leghatékonyabban tölthetik ki a magok a rendelkezésre álló területet.
Némi kutatómunkával, a legszabályosabb egyedek megfelelő szögből történő lefényképezésével könnyen lehet találni olyan spirális alakzatokat, amelyek tökéletesen követik az arany spirált (ahogyan rengeteg olyat is, amelyek más spirál alakzatokat követnek), de a természet ritkán produkál matematikai tökéletességet, elég ha páros szerveink eltéréseire gondolunk.
A művészeti alkotások kapcsán, ahol a kompozíció eleve megkövetel az alkotótól bizonyos aránytartásokat, szintén lehet találni példákat az aranyspirálra, illetve az aranyszámmal, a Fi-vel leírható aránypárokra. Ahogyan olyanokat is, ahol még véletlenül sem találjuk őket.
🌸
Ki volt Fibonacci?
Az 1170 és 1250 között élt itáliai matematikus, Leonardo di Pisa (ma ismert nevén Leonardo Fibonacci) valószínűleg sosem gondolta volna, hogy az internet és a kreacionizmus látens híveinek köszönhetően ilyen legendássá válik az egyébként már a 6. századi Indiában is ismert számsorozat.
A XII. század Itáliájában még mindig a római számokat használták, amely igencsak megnehezítette a számokkal foglalkozók, elsősorban kereskedők életét. Leonardo maga is megtapasztalhatta ezt, amikor apjának segített, aki kereskedelmi ügyvivő volt az Almohád-Dinasztia szultánusában, a mai Algéria területén. Itt botlott bele az ifjú Leonardo az arabok által használt tízes számrendszerbe, amellyel sokkal egyszerűbben és hatékonyabban lehetett számolni.
Több arab matematikusnál tanult, hogy minél jobban elmélyedjen a tízes számra az arab számok tudományában, majd 1200 körül hazatérve Liber Abaci című művében kezdje népszerűsíteni azokat.
A könyv a tízes számrendszer és vele való műveletek ismertetésén túl számos gyakorlati útmutatót kínált az élet különböző területeire, a súlyok és mértékegységek átváltásától a tőkekalkulációkon keresztül egészen a nyúltenyészet elméleti növekedési görbéjének meghatározásáig. Ez utóbbihoz használt, meglehetősen erőltetett példával vezette be az európai köztudatba az azóta misztikussá váló számsort, amelyet az iránta való tiszteletből róla neveztek el.
Miért vannak jelen mindenütt?
Valójában éppannyira vannak jelen, mint számos egyéb mintázat, amelyet matematikai modellekkel le tudunk írni. A misztikum azonban, amelyre cikkünk elején mi is példákat hoztunk fel, nem más, mint szemfényvesztés, egyszerű bűvészmutatvány. Kiragadott példákat kerestünk a Fibonacci számokra illetve a Fibonacci spirálra, nagyvonalúan elfeledkezve mindazon esetekről, amikor a Fibonacci rejtélyt semmilyen módon sem tudnánk ráerőltetni a természetre.
33 darab csigolyánk van, nyakcsigolyánk 7, hátcsigolyánk pedig 12. Egyikük sem Fibonacci szám. Ahogyan számos virágnak a Fibonacci számtól eltérő számú szirma van (pl. liliom 6, gardénia 9, hegyi babér 10).
Nem magyaráztuk meg, miért 12 hangból áll egy oktáv, ahogyan azt sem, hogy a fülbemászó melankolikus dallamok elengedhetetlen kelléke, a moll akkord miért az 1-ső 4-dik és 8-dik (sic!) billentyű lenyomásával szólaltatható meg.
Szándékosan elfelejtettük megemlíteni a számsor néhány fontos matematikai törvényszerűségét. Egyrészt, hogy bármely egész szám felírható Fibonacci számok segítségével, másrészt bármely szám előállítható két vagy több olyan Fibonacci szám összeadásával, amelyek nem szomszédai egymásnak. Így nem okozott különösebb nehézséget a 42-t egymást követő, illetve egymással nem szomszédos Fibonacci számokból előállítani.
A spirális alakzatok tekintetében szintén csaltunk. Szándékosan olyan képeket közöltünk, ahol szabad szemmel nem megállapítható a különbség, csak ha egymásra tennénk a képet és a spirált.
A Fibonacci spirált gyakran hasonlítják az ún. aranyspirálhoz, amely nem más, mint az aranymetszésből ismert Fibonacci alapú logaritmikus spirál. Természettudósok szerint a logaritmikus spirál mintázatát valóban sok élőlény próbálja követni, azon egyszerű oknál fogva, hogy ez a legjobb módszer az arányos növekedésre, a napraforgó tányérja esetében pedig megközelítőleg a leghatékonyabban tölthetik ki a magok a rendelkezésre álló területet.
Némi kutatómunkával, a legszabályosabb egyedek megfelelő szögből történő lefényképezésével könnyen lehet találni olyan spirális alakzatokat, amelyek tökéletesen követik az arany spirált (ahogyan rengeteg olyat is, amelyek más spirál alakzatokat követnek), de a természet ritkán produkál matematikai tökéletességet, elég ha páros szerveink eltéréseire gondolunk.
A művészeti alkotások kapcsán, ahol a kompozíció eleve megkövetel az alkotótól bizonyos aránytartásokat, szintén lehet találni példákat az aranyspirálra, illetve az aranyszámmal, a Fi-vel leírható aránypárokra. Ahogyan olyanokat is, ahol még véletlenül sem találjuk őket.
🌸
🌸
🌸
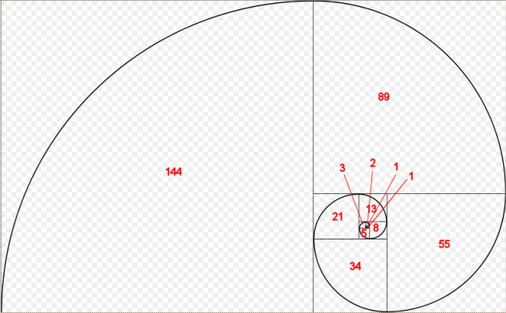
A fekete spirál a Fibonacci, a piros pedig a szabályos aranyspirál.
Különösen az elején látható a különbség.
A Fibonacci egy irracionális szám, közelítő értékkel 1,618, reciproka pedig 0,618. A Fibonacci számsor elemeire 55-től kezdődően valóban igaz, hogy az egymást követő számok hányadosai egyre jobban közelítik ezt az értéket, ebből adódóan a Fibonacci spirál és az aranyspirál között csak közelebbről szemügyre véve vehető észre a különbség.
Ám a Fibonacci számsor logikája alapján előállított bármely más számsorral is ugyanezt az arányt kapjuk. Próbáljuk ki például a 6, 7, 13, 20, 33, 53, 86, 139, 225, 364, 589 számsort. 225-től kezdődően ugyanúgy Fibonaccit közelítő értékeket kapunk.
🌸
Ha egy élethű fát, vagy virágszirmot akarunk rajzolni, vagy biztosra akarunk menni egy kép beállításánál, a fenti arányok figyelembevételével biztosan nem lövünk mellé.
A fekete spirál a Fibonacci, a piros pedig a szabályos aranyspirál.
Különösen az elején látható a különbség.
A Fibonacci egy irracionális szám, közelítő értékkel 1,618, reciproka pedig 0,618. A Fibonacci számsor elemeire 55-től kezdődően valóban igaz, hogy az egymást követő számok hányadosai egyre jobban közelítik ezt az értéket, ebből adódóan a Fibonacci spirál és az aranyspirál között csak közelebbről szemügyre véve vehető észre a különbség.
Ám a Fibonacci számsor logikája alapján előállított bármely más számsorral is ugyanezt az arányt kapjuk. Próbáljuk ki például a 6, 7, 13, 20, 33, 53, 86, 139, 225, 364, 589 számsort. 225-től kezdődően ugyanúgy Fibonaccit közelítő értékeket kapunk.
🌸
Ha egy élethű fát, vagy virágszirmot akarunk rajzolni, vagy biztosra akarunk menni egy kép beállításánál, a fenti arányok figyelembevételével biztosan nem lövünk mellé.
🌸
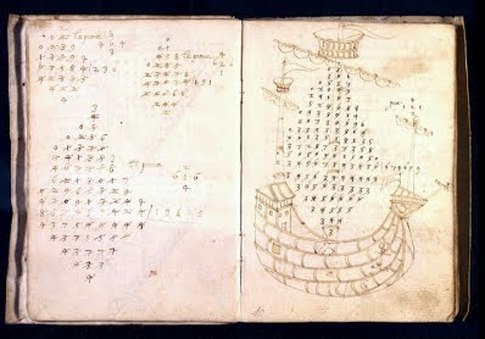
Fibonacci / Liber Abaci (Könyv az Abakuszról) Című Könyve
🌸
Fibonacci / Liber Abaci (Könyv az Abakuszról) Című Könyve
🌸
(1887-1965)
Le Corbusier / Charles - Édouard Jeanneret - Gris
Svájci - Francia építész, tervező, festő, várostervező, író,
és az egyik híres úttörője a modern építészetnek.
Született: Október 6, 1887, La Chaux - de - Fonds, Svájcban
Meghalt: Augusztus 27, 1965, Roquebrune - Cap - Martin, Franciaországban
Le Corbusier szerint a világegyetem rendje szorosan összekötődik az
aranymetszés és a Fibonacci számokkal, ahol a ritmusok szembetűnőek
és világosan kapcsolodnak egymással.
A "Der Modulor" című könyvében Le Corbusier kifejezetten használja az aranymetszést.
Követte Leonardo da Vinci "Vitruvius" munkáját aki használta az arany arányt.
Le Corbusier szerint ez a rendszer a Fibonacci számok.
Svájci - Francia építész, tervező, festő, várostervező, író,
és az egyik híres úttörője a modern építészetnek.
Született: Október 6, 1887, La Chaux - de - Fonds, Svájcban
Meghalt: Augusztus 27, 1965, Roquebrune - Cap - Martin, Franciaországban
Le Corbusier szerint a világegyetem rendje szorosan összekötődik az
aranymetszés és a Fibonacci számokkal, ahol a ritmusok szembetűnőek
és világosan kapcsolodnak egymással.
A "Der Modulor" című könyvében Le Corbusier kifejezetten használja az aranymetszést.
Követte Leonardo da Vinci "Vitruvius" munkáját aki használta az arany arányt.
Le Corbusier szerint ez a rendszer a Fibonacci számok.
Le Corbusier Híres Tervezései:
Az Egyesült Nemzetek Székhelye, New York, USA. 1947
Chapel of Notre Dame du Haut, Ronchamp, France. 1954
Az Egyesült Nemzetek Székhelye, New York, USA. 1947
Chapel of Notre Dame du Haut, Ronchamp, France. 1954
🌸
Kép az "Open Hand" (La Main ouverte) Le Corbusier Alkotása:
A "Béke és Megbékélés Szimbóluma"
26 méter magas, Indiában / Chandigar Városában Található
Kép az "Open Hand" (La Main ouverte) Le Corbusier Alkotása:
A "Béke és Megbékélés Szimbóluma"
26 méter magas, Indiában / Chandigar Városában Található